On power and the 'match point situation'
We all have seen the opening scene from Woody Allen’s movie Match Point (2005)
The man who said “I’d rather be lucky than good” saw deeply into life. People are afraid to face how great a part of life is dependent on luck. It’s scary to think so much is out of one’s control. There are moments in a match, when the ball hits the top of the net, and for a split second, it can either go forward or fall back. With a little luck, it goes forward, and you win. Or maybe it doesn’t, and you lose.
In this post I will argue that the match point situation (i.e., a situation in which your entire life is dictated by chance only), is a common situation for the researcher who uses Null Hypothesis Significance Testing (NHST) without controlling power.
What is power?
As experimentalists, we are lead to discuss the plausibility of theories in the light of new incoming data. At least, this is what we would like to do. Rather, using NHST, we are usually doomed to discuss the plausibility of the observed data (or more extreme data), given that the null hypothesis H0 is true (is it?).
In doing this, there are two imaginable outcomes: either we reject H0, or we do not. Two kind of errors1 can be made when one makes this decision:
Type I errors. This is the rate of false positives in the long-run. In other words, how many times you will reject the hypothesis according to which there is no effect while actually… there is no effect.
Type II errorss. This is the rate of false negatives, which correponds to failing to reject the null hypothesis, while you should have rejected it.
The subsequent table summarises four possible outcomes of a test, according to the population value of the effect size and the decision you have made.
| H0 (\(\delta = 0\)) | H1 (\(\delta \neq 0\)) | |
|---|---|---|
| Reject H0 | Type I error | Correct inference |
| Fail to reject H0 | Correct inference | Type II error |
Generally speaking, power is the probability of achieving a specified goal. In the context of NHST, statistical power is usually defined as the probability of detecting an effect (i.e., rejecting the null) if there really is an effect.
Experimenting power by yourself
Below you can find an interactive visualisation of the p-value distribution (in the simple case of an independent-samples t-test), according to the effect size (Cohen’s d), the sample size, and the alpha level. You can play with these values to see how the distribution of p-values is affected.
Interestingly, we realise that playing with these different parameters modifies the statistical power, which is the ability to detect an effect if there is a true effect (i.e., a difference in the population).
Intuitively, after playing with several values of \(d\) and \(n\), you should be able to formulate your own definition of what power is…
Here are some clues: try to fix \(d=0.3\) and \(n=20\)… power should be around 15%. Then, with the same effect size (\(d=0.3\)), try to increase the sample size at \(n=40\). Power should now be around 25%. You should be able to see that the power is nothing more than the proportion of p-values that fall below the \(\alpha\) level you fixed. Thus, power also depends on the risk of false positives you are ready to take.
empirical_power <- (sum(p < alpha) / number_of_experiments)
From this interactive widget, we learned that for a Cohen’s \(d\) of 0.3, with 40 participants, power is around 0.25. What does it mean? The interpretation of this number is quite straightforward: we have only 1 chance out of 4 to find a significant effect in our experiment, while there really is an effect…!2
The problem with low power: the match point situation
The average published effect size in psychology is around \(d=0.5\), with a typical power of 0.35 (Bakker et al., 2012, 2016). Slowly, we see that things are evolving and improvements have been made but still, power is rarely something we care about and is rarely above 0.5.
When you have a power of 0.5, it means that the chances of detecting the effect you are looking for are no more important than the chances to get a head when flipping a coin…! These chances are neither no more than the tennis ball passing over the net or staying on your side…
Are you really ready to give up on several months (or years) of work on a coin toss?
Why we do not care
I think the main problem is that we do not realise how bad is low power. We generally have very poor intuitions when it comes to estimating the real power of a specific experiment (e.g., see Bakker et al., 2016). More generally, it is well acknowledged that we are really bad at understanding how chance and random processes can affect hypothesis testing, as illustrated by the famous law of small numbers of Tversky & Kahneman (1971).
Here is an excerpt:
In review, we have seen that the believer in the law of small numbers practices science as follows:
- He gambles his research hypothesis on small samples without realizing that the odds against him are unreasonably high. He overestimates power.
- He has undue confidence in early trends (e.g., the data of the first few subjects) and in the stability of observed patterns (e.g., the number and identity of significant results). He overestimates significance.
- In evaluating replications, his or others’, he has unreasonably high expectations about the replicability of significant results. He underestimates the breadth of confidence intervals.
- He rarely attributes a deviation of results from expectations to sampling variability because he finds a causal “explanation” for any discrepancy. Thus, he has little opportunity to recognize sampling variation in action. His belief in the law of small numbers, therefore, will forever remain intact.
What can we do?
There is some hope though! Let’s remember the interactive shiny widget you have played with two minutes ago (above). The easiest way to increase power is simply to increase sample size.
In a practical ground, when doing a priori power analyses, in order to define the sample size of your next experiment, one resourceful idea would be to use safeguard power analysis rather than the classical power analysis (Perugini et al., 2014). Basically, this method consists in computing a confidence interval around the targetted effect size and to make classic power analyses based on the lower bound of the interval. Results of the simulation presented by the authors of this paper are quite convincing in increasing the real power of studies. Obviously, the conclusions here are the same as before: we should increase our sample size.
Another advocated approach is to plan for estimation precision, rather than planning for rejecting the null. This is the the goal is accuracy of Krushke (2015, chapter 13). In this case, we will never falsely reject the null or the alternative, and this procedure will give virtually unbiased parameter estimates. However, this sweet thing comes with a price. We will sometimes remain uncertains (i.e., unable to make a decision), and always need bigger sample sizes.
A last tip would be to ask the question in a slightly different way Why do we have to bother with a priori power? Why could not we recruit participants until we have enough data/evidence to make our point?
Sequential testing
Sequential analysis simply refers to the process by which one collects data (e.g., recruits participants) until reaching a predefined level of evidence. One implementation of this idea has been proposed by Wald (1945) and is known as the Probability Ratio Test. Apart from the Wald test, the most NHST common sequential designs are called group sequential designs and the interested reader will be delighted to find more information in Lakens & Evers (2014), or Schönbrodt and colleagues (2015).
Time to step on the Bayesian side. This animation is taken from the BFDA package (Schönbrodt, 2016).
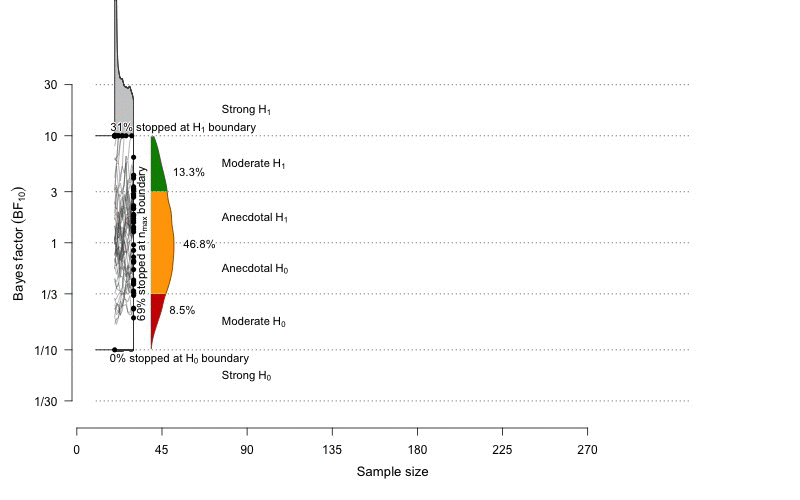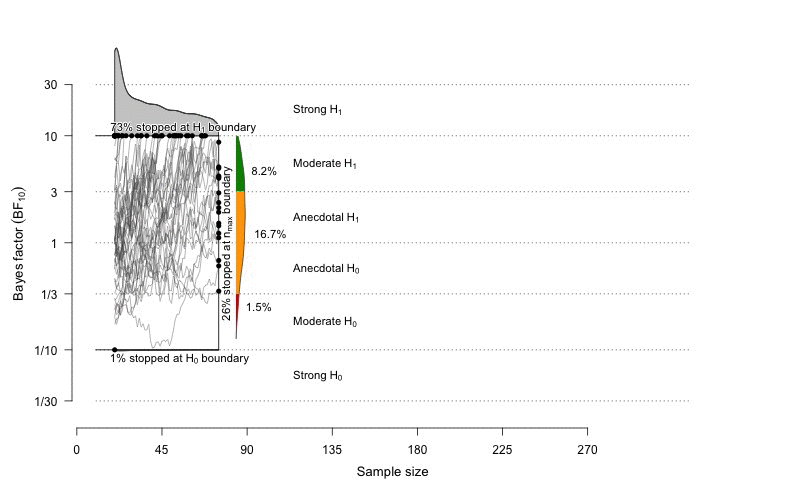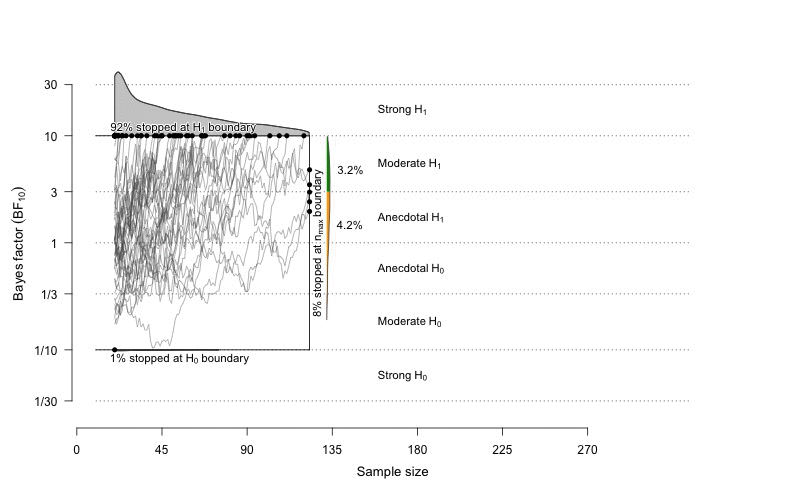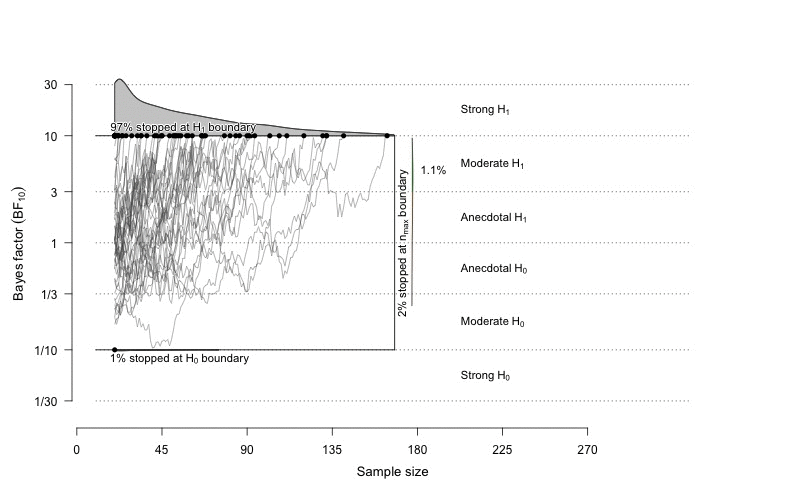
On this illustration, we can see the results of the computation of sequential Bayes factors as we increase the sample size (on the x-axis). Each grey line represents the value of a Bayes factor computed in one simulation of a fictive experiment for a given effect size and for a given sample size. Upper and lower boundaries are fixed to \(BF_{10}=10\) and \(BF_{10}=1/10\). These boundaries represent the level of evidence at which we would stop the experiment.
Sequential testing does not eliminate the question of power, it just asks a lishtly different question. The question is no more to decide a priori on a fixed sample size in order to have a fixed probability to find an effect if this effect really exists. Rather, sequential testing allows running the experiment as long as we do not reach a predefined level of evidence (e.g., BF = 20). By means of simulation we can then evaluate the long-term rates of false-positive or false-negative evidence (see Schönbrodt et al., 2015; Schönbrodt & Wagenmakers, 2016). If we decide to be very demanding concerning the level of evidence, eventually, as \(N\) increases, the power will tend to 100%. As a fatal argument, I should tell you that, comparing to NHST, Bayesian sequential testing with Bayes factors typically needs 50% to 70% smaller samples to reach a conclusion, while having the same or lower long-term rate of wrong inference (Schönbrodt et al., 2015).
Moreover, Bayesian sequential testing does not suffer from the problems associated with sequential testing in the frequentist framework3. In accordance with the statement of Edwards et al. (1963), “the rules governing when data collection stops are irrelevant to data interpretation. It is entirely appropriate to collect data until a point has been proven or disproven, or until the data collector runs out of time, money, or patience”.
Wait, wouldn’t be what we are looking for? It seems legitimate to ask whether it is a better strategy to collect data until sufficient evidence has been accumulated or to collect data until an a priori fixed \(N\), ensuring that we have a fixed probability to reject an highly improbable null hypothesis…
References
Click to expand
Aronson, L., Wiley, G., Darwin, L., & Allen, W. (2005). Match Point. United States: DreamWorks Pictures, United Kingdom: Icon productions.
Bakker, M., van Dijk, A., & Wicherts, J. M. (2012). The rules of the game called psychological science. Perspectives on Psychological Science, 7, 543–554. https://doi.org/10.1177/1745691612459060
Bakker, M., Hartgerink, C. H. J., Wicherts, J. M., & Maas, H. L. J. Van Der. (2016). Researchers’ Intuitions About Power in Psychological Research. Psychological Science, 27(8), 1069–1077. http://doi.org/10.1177/0956797616647519
Edwards, W., Lindman, H., & Savage, L. J. (1963). Bayesian statistical inference for psychological research. Psychological Review, 70, 193-242.
Kruschke, J. K. (2011). Bayesian assessment of null values via parameter estimation and model comparison. Perspectives on Psychological Science, 6, 299–312. http://doi.org/10.1177/1745691611406925
Perugini, M., Gallucci, M., & Costantini, G. (2014). Safeguard Power as a Protection Against Imprecise Power Estimates. Perspectives on Psychological Science, 9(3), 319–332. http://doi.org/10.1177/1745691614528519
Schönbrodt, F. D., Wagenmakers, E.-J., Zehetleitner, M., & Perugini, M. (2015). Sequential hypothesis testing with Bayes factors: Efficiently testing mean differences. Psychological Methods. http://dx.doi.org/10.1037/met0000061
Schönbrodt, F., & Wagenmakers, E.-J. (2016). Bayes factor design analysis: Planning for compelling evidence. Manuscript submitted for publication. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2722435
Tversky, A., & Kahneman, D. (1971). Belief in the law of small numbers. Psychological Bulletin, 76(2), 105-110. http://dx.doi.org/10.1037/h0031322
Wagenmakers, E.-J. (2007). A practical solution to the pervasive problems of p values. Psychonomic Bulletin & Review, 14(5), 779–804.
Notes
Note that there are several others (and arguably more important) errors that one can make when it comes to inference, like type-M or type-S errors, but see this paper for more details.↩︎
See also this similar but much more pretty and elaborated visualisation of the p-values distribution on R psychologist.↩︎
These problems would also need an entire topic. For an introduction, see Wagenmakers (2007).↩︎